This post is motivated by the Euler project’s third problem, finding the largest prime factor of the number n=600,851,475,143. In my humble opinion, the most challenging issue of the problem is how to efficiently determine whether a number is prime, and the best candidate is the sieve of Eratosthenes algorithm. In other words, my strategy is:
- Generate all prime numbers up to the given
nto ensure a fixed time (i.e.,O(1)) for prime-checking. - If
nis a prime number, returnn. - Otherwise, for each prime number
p(found in step 1):- If
nis divisible byp, letn = p * n'and setans = p- If
n'is also a prime numbers, the returnmax(ans, n'). - Otherwise, set
n = n'and continue the loop.
- If
- Otherwise, continue the loop.
- If
- return
ans.
This post focuses on the frist step (i.e, generating prime numbers). Thus, I present the sieve of Eratosthenes algorithm and C++ implementations with different optimizations.
The sieve of Eratosthenes
The sieve of Eratosthenes is an ancient algorithm to find all the prime numbers less than or equal to a given integer n. The detail of the algorithms is as follows:
- Create an array of consecutive integers from
2ton. - Take the first element of the array (i.e.,
2) and mark all other elements which are multiples of the element (except itself) asnonprime. - Repeat step 2 for the next element that has not been marked until reaching
n.
C++ implementations
Version 1
In this version, I simply implement the algorithm with a minor optimization. Instead of using an array of consecutive integers, I use an array of boolean variables (named primes) to indicate whether a number is prime. That is, if primes[i] == true , then i is a prime number. The detail of of the implementation is as follows:
#include <algorithm>
#include <memory>
unique_ptr<bool[]> create_SoE_v1 (const size_t &n) {
unique_ptr<bool[]> primes{ make_unique<bool[]>(n+1)};
fill_n(primes.get(), n+1, true);
// 0 and 1 are not considered as prime numbers
primes[0] = false;
primes[1] = false;
// Mark non-prime numbers
for(size_t i = 2; i <= n; i++) {
if(primes[i] == true) {
for(size_t j = 2*i; j <= n; j += i) {
primes[j] = false;
}
}
}
return move(primes);
}
As denoted in the following table, the algorithm can find about 455 million prime numbers between 2 and 10 billion in about 2 mins when running on my Dell Precision 5820 PC (Intel(R) Xeon(R) 3.20GHz CPU and 32GB of RAM). Although this is quite good, it is still quite far from my goal, as I also got a memory error when n is 100 billion.
| n | # of prime numbers | Time (s) |
|---|---|---|
| 10,000,000 | 664,579 | 0.82 |
| 100,000,000 | 5,761,455 | 8.59 |
| 1000,000,000 | 50,847,534 | 93.31 |
| 10,000,000,000 | 455,052,511 | 130.19 |
| 100,000,000,000 | memory error | |
Version 2
Observe that:
- If
nis not a prime number, I can always find a pair of integerspandqsuch that bothpandqare less thann, andpis a prime number. - If
nis a prime number, the algorithm ensures that all nonsize_t-prime numbers smaller thatnare marked.
Thus, instead of checking all the way up to n, I need to check up to only the square root of n. Here is the new implementation:
unique_ptr<bool[]> create_SoE_v2(const size_t &n) {
unique_ptr<bool[]> primes{ make_unique<bool[]>(n+1)};
fill_n(primes.get(), n+1, true);
// 0 and 1 are not considered as prime numbers
primes[0] = false;
primes[1] = false;
// Mark non-prime numbers
size_t sqrt_n = static_cast<size_t>(sqrt(n));
for (size_t i = 2; i <= sqrt_n; i += 2) {
if(primes[i] == true) {
for(size_t j = 2*i; j <= n; j += i) {
primes[j] = false;
}
}
}
return move(primes);
}
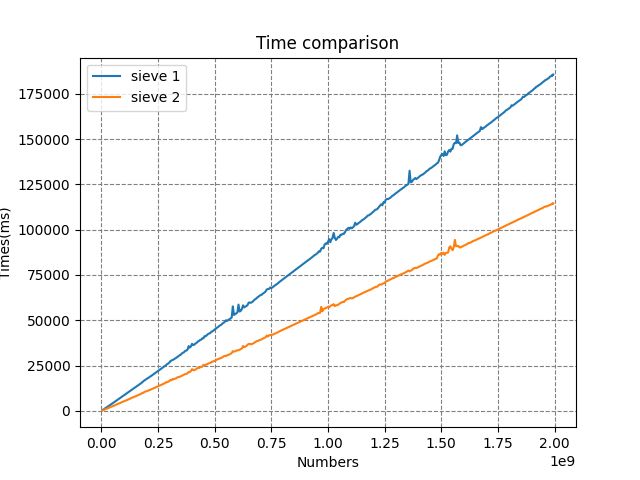
This version is approximately one third faster than the first one, as denoted in Figure 1. However, it still produces the memory error when n is 100 billion.
Version 3
In this version, I aim to optimize the memory by replacing the boolean variables with bits. A simple approach is to utilize the built-in bitset class, but the set’s length must be provided at compiling time, which I do not like. So, I develop a new solution using an array of std::byte’s. That is, I will divide the numbers into groups of 8 elements and have each bit of the corresponding std::byte indicating whether an element of the group is prime or not. Note that when n is not divisible by 8, the last group is not full, so we must clean the trailing bits.
Additionally, except 2, there is no other prime number that is even. Thus, I can ignore all even numbers and have the array start from 3. This optimization helps to reduce not only half of the required memory but also the number of loops. Without further ado, here is the major part of the third implementation:
SoE(const size_t &n): m_upper_bound(n){
size_t number_of_blocks = (((n >> 1) - 1) >> 3) + 1;
m_primes = make_unique<byte[]>(number_of_blocks);
fill_n(m_primes.get(), number_of_blocks, static_cast<byte>(0xFF));
// a lambda to check whether number at index is prime
auto check = [&](const size_t &index) {
size_t block_index = ((index >> 1) - 1) >> 3;
size_t offset = ((index >> 1) - 1) & 0x7;
byte mask{0x80};
mask >>= offset;
return to_integer<int>(m_primes[block_index] & mask) > 0;
};
// a lambda to clear the bit at index
auto mark = [&](const size_t &index) {
size_t block_index = ((index >> 1) - 1) >> 3;
size_t offset = ((index >> 1) - 1) & 0x7;
byte mask{0x80};
mask >>= offset;
m_primes[block_index] &= ~mask;
};
// Clear trailing bits
size_t last_group_size = ((n >> 1) - 1) & 0x7;
byte mask{0xFF};
mask >>= last_group_size;
m_primes[number_of_blocks - 1] ^= mask;
// Mark non-prime numbers
size_t sqrt_n = static_cast<size_t>(sqrt(n));
for (size_t i = 3; i <= sqrt_n; i += 2) {
if (check(i)) {
for (size_t j = 3 * i; j <= n; j += 2*i) {
mark(j);
}
}
}
};
As you may notice, I also had some minor optimization by using bitwise operators instead of division and modulo.
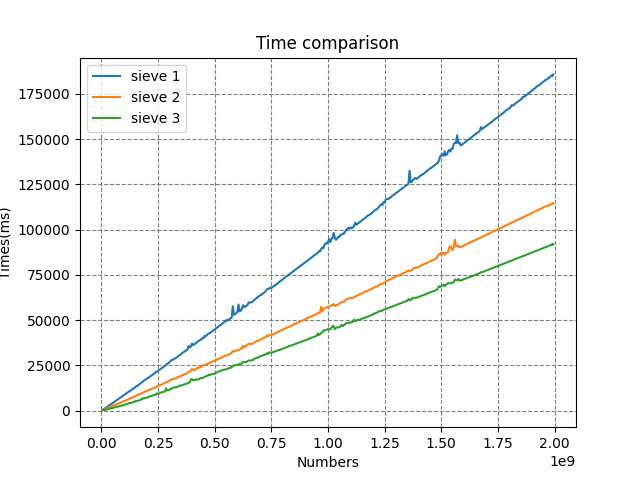
The time comparison between the three versions is shown in Figure 2, and the last version, of course, outperforms the other two. Additionally, this is also the only one that can find all prime numbers between 2 and 250 billion (taking about 5 hours), which is still quite far from my goal.
At this point, I am thinking of parallelizing the algorithm. That is, I will divide the range into smaller segments and process them in parallel. However, the latter segments likely have less prime numbers than the former ones making threads processing latter segments have to invoke the mark lambda more often than those of former segments. In other words, the challenge of parallelizing the algorithm is how to balance the workload between threads. Thus, I would like to have these kinds of optimization in a separate post.
Conclusion
This post presented the accent algorithm named Sieve of Eratosthenes and 3 different implementations in C++, optimizing running time and storing space. Although the original goal is to find all prime numbers between 2 and 600,851,475,143 to solve the Euler project’s third problem, the proposed implementation can only do [2, 250,000,000,000]. Another possible optimization is to divide the range into smaller segments and process them in parallel, which I will present in another post soon.
Finally, the source code of the implementations can be found here.